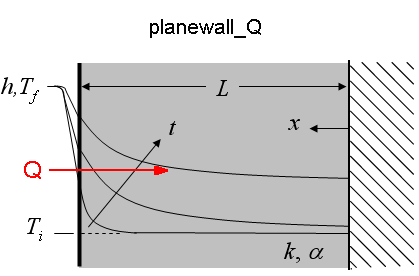
Planewall_Q

The function planewall_Q(time, T_i, T_f, alpha, k, h, L) returns the heat transfer per unit area ([J/m^2 or Btu/ft^2]) for a bounded plane wall exposed to convection at one surface (x=L) and adiabatic at the other surface (x=0)
Inputs:
time - time relative to beginning of convection [sec]
T_i - initial temperature of plane wall [C], [K], [F], or [R]
T_f - bulk fluid temperature [C], [K], [F], or [R]
alpha - thermal diffusivity [m^2/s] or [ft^2/hr]
k - thermal conductivity of plane wall [W/m-K] or [Btu/hr-ft-R]
h - heat transfer coefficient [W/m^2-K] or [Btu/hr-ft^2-R]
L - thickness of plane wall [m] or [ft]
Notes:
Function planewall determines the Biot and Fourier numbers and calls the function planewall_Q_ND, which determines the non-dimensional heat transfer, Q_hat. Q_hat is then multiplied by the maximum heat transfer to obtain planewall_Q, as explained in section 3.5.2 of Nellis and Klein.
Example:
$UnitSystem SI K Pa J
time=5000 [sec]
T_i=303 [K]
T_f=363 [K]
alpha=8.608e-5 [m^2/s]
k= 233 [W/m-K]
h= 50 [W/m^2-K]
L= 0.5 [m]
Q=planewall_Q(time, T_i, T_f, alpha, k, h, L)
{Solution: q``=1.328E+07 [J/m^2]}