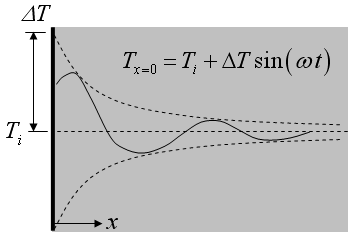
Periodic Temperature

Function semiinf5(T_i,DeltaT,omega,alpha,x,time) returns the temperature for a given position and time within a semi-infinite body with a sinusoidally varying surface temperature using the relation provided in Table 3-2 of Nellis and Klein.
Inputs:
T_i - initial temperature of the solid [C] or [K]
DELTAT - amplitude of surface temperature variation [C] or [K]
omega - angular velocity [rad/s]. The surface temperature is T_i+DELTAT*sin(omega*time)
alpha - thermal diffusivity (m^2/s)
x - perpendicular distance from surface [m]
time - time relative to impulse (energy impulse occurs at t=0) [s]
Example:
$UnitSystem SI K Pa J
T_i=293 [K]
DELTAT=15 [K]
omega=7.272 [rad/s]
c=383 [J/kg-K]
alpha=0.00011 [m^2/s]
x=0.01 [m]
time=0.5 [s]
T=semiinf5(T_i,DeltaT,omega,alpha,x,time)
{Solution: T=T=295.4 [K]}