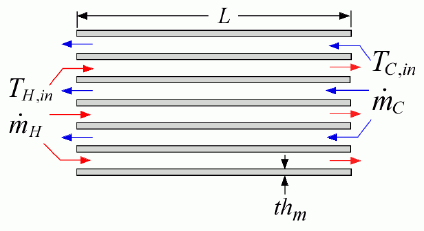
AxialConductionHX

SUBPROGRAM AxialConductionHX provides a finite difference analysis of a counterflow heat exchanger with a consideration of axial conduction in the manner described in section 8.6.4 of Nellis and Klein.
Inputs:
C_dot_H hot-side fluid capacity rate (W/K)
C_dot_C cold-side fluid capacity rate (W/K)
NTU_H hot side NTU (ratio of hot side conductance to hot side capitance rate)
NTU_C cold side NTU (ratio of cold side conductance to cold side capitance rate)
lambda axial conduction parameter
gamma concentration parameter for node distribution (0 = uniform grid; 1 is a reasonable value)
Outputs:
eff effectiveness of the heat exchanger
eff_nac effectiveness of the heat exchanger if axial conduction is not considered
Notes:
The numerical model uses 500 nodes with an exponential spacing that concentrates nodes at the ends of the heat exchanger. The spacing is controlled by the value of input gamma. If the value of gamma is set to 0, the grid will be uniform. Increasing values of gamma providing more nodes at the ends of the heat exchanger.
C_dot_H is the product of the mass flow rate and specific heat capacity of the hot fluid. C_dot_C is defined in the same manner.
NTU_H is the ratio of the conductance (heat transfer coefficient - area product) on the hot fluid side to the hot fluid capacitance rate. NTU_C is defined in the same manner.
The units of the inputs and outputs to this Subprogram must be as indicate above, regardless of the settings in the EES unit system dialog.
Example:
$unitSystem SI J K Pa
C_dot_H=130 [W/K] "hot fluid capacitance rate"
C_dot_C=130 [W/K] "cold fluid capitance rate"
NTU_H=90 [-] "hot fluid NTU"
NTU_C=90 [-] "cold fluid NTU"
lambda=0.1 "axial conduction parameter defined in section 8.7"
gamma=2 "concentration parameter for node distribution"
Call AxialConductionHX( C_dot_h, C_dot_c, NTU_h, NTU_c, lambda,gamma: eff, eff_nac)
{Solving results in eff=0.899 and eff_nac=0.978}