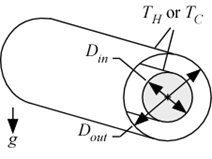
FC_Annular_Enclosure

Procedure FC_Annular_Enclosure(Fluid$, T_h, T_c, P, Dout, Din : hc, Nusselt, Ra) returns the heat transfer coefficient in an annular space that is formed between two concentric horizontal cylinders.
Note that the area of the inner cylinder should be used when computing heat transfer rate.
The correlation that is used is from Barron and Nellis, Cryogenic Heat Transfer, 2nd Edition, CRC Press, 2016.
See FC_Annular_Enclosure_ND for a non-dimensional correlation for this geometry.
Inputs:
Fluid$: can be any fluid in the EES data base (including ideal gas or real fluid)
T_h - temperature of one of the cylinders in [C], [K], [F], or [R]
T_c - temperature of the other cylinder in [C], [K], [F], or [R]
P - absolute pressure in [Pa], [kPa], [bar], [MPa], [atm], or [psia]
Dout -outer cylinder diameter [m] or [ft]
Din - inner cylinder diameter [m] or [ft]
Outputs:
hc - heat transfer coefficient in [W/m^2-K] or [Btu/hr-ft^2-R]
Nusselt - Nusselt number [-]
Ra - Raleigh number [-]
Example:
$UnitSystem SI Mass J K Pa
Dout=0.1615 [m] "outer pipe diameter"
Din=0.1143 [m] "inner pipe diameter"
H=12 [m] "pipe length"
T_h=300 [K] "hot temperature"
T_c=90 [K] "cold temperature"
P=101325 [Pa] "pressure"
F$='Nitrogen' "fluid"
Call FC_Annular_Enclosure(F$, T_h, T_c, P, Dout, Din : hc, Nusselt, Ra)
Ain=Din*H*pi "surface area of inner pipe"
Q_dot=Ain*hc*(T_h-T_c) "heat transfer rate"
{Solution
hc = 6.582 [W/m^2-K]
Q_dot = 5956 [W]}