External_Flow_Square

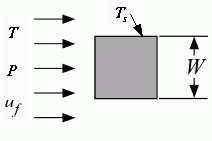
Procedure External_Flow_Square(Fluid$, T_inf, T_s, P, u_inf, W: F_d\L, h, C_d, Nusselt, Re) calculates the average heat transfer coefficient and drag force per unit length of a square-shaped rod as well as the drag coefficient, Nusselt and Reynolds numbers. The properties are evaluated at the film temperature and the units of the inputs and outputs correspond to the settings in EES.
Inputs
Fluid$ can be any fluid in the EES data base. The fluid can be an ideal gas, a real fluid, a brine, or an incompressible fluid in the Solid-Liquid_Props fluids library.
T_inf - the free stream fluid temperature in [C], [K], [F], or [R].
T_s - the surface temperature of the rod in [C], [K], [F], or [R].
P - pressure can be in [Pa], [kPa], [bar], [MPa], [atm] or [psia]. (Note that for brines, this parameter provides the concentration in % instead of pressure.)
u_inf - free stream velocity of the flow in [m/s] or [ft/min]
W - height of the side of the rod in [m] or [ft]
L - length of the rod in [m] or [ft]
Outputs
F_d\L - drag force in [N/m] or [lb_f/ft]
h - average heat transfer coefficient in [W/m^2-K] or [Btu/hr-ft^2-R]
C_d - drag coefficient [-], which is defined as
![]() ,
,
where
Afr is the frontal area,
r is the density
Nusselt - average Nusselt number [-], defined as
![]()
where
k is the conductivity
Re - Reynolds number [-], defined as
![]()
where
m is the viscosity
Notes
This procedure is responsible for determining the property data of the fluid specified and calculating the Reynolds and Prandtl numbers. This procedure then passes the Reynolds and Prandtl numbers to the non-dimensional procedure External_Flow_Square_ND. The non-dimensional procedure returns the values for C_d and Nusselt. This procedure uses the Nusselt number and drag coefficient to calculate the drag force and the convection heat transfer coefficient.
Example
$UnitSystem SI K Pa J
T_s=328 [K]
Fluid$='air'
T_inf=297 [K]
P=101300 [Pa]
u_inf=10 [m/s]
W=0.01 [m]
Call External_Flow_Square(Fluid$, T_inf, T_s, P, u_inf, W: F_d\L, h, C_d, Nusselt, Re)
{Solution: F_d\L=1.186 [N/m], h=85.42 [W/m^2-K], C_d=2.1 [-]}