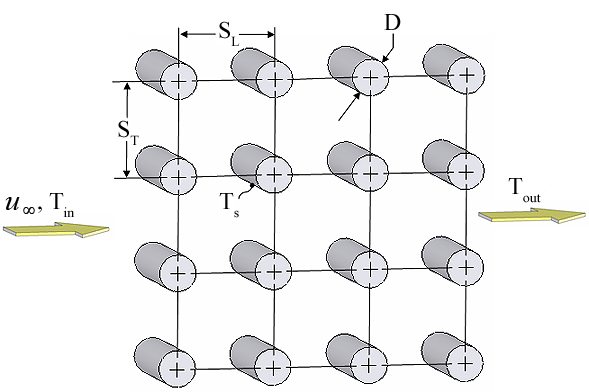
External_Flow_Inline_Bank

Procedure External_Flow_Inline_Bank(Fluid$, T_in, T_out, T_s, P, u_inf, N_L, D,S_T,S_L: h, DELTAp, Nusselt, Re) calculates the average heat transfer coefficient, and total pressure drop over an inline bank of tubes. Properties are evaluated at the film temperature and the units of the inputs and outputs correspond to the settings in EES.
Inputs
Fluid$ can be any fluid in the EES data base. The fluid can be an ideal gas, a real fluid, a brine, or an incompressible fluid in the Solid-Liquid_Props fluids library.
T_in - the free stream fluid temperature at the inlet in [C], [K], [F], or [R].
T_out - the free stream fluid temperature at the outlet in [C], [K], [F], or [R].
T_s - the surface temperature of the sphere in [C], [K], [F], or [R].
P - pressure can be in [Pa], [kPa], [bar], [MPa], [atm], or [psia]. (Note that for brines, this parameter provides the concentration in % instead of pressure.)
u_inf - free stream velocity of flow in [m/s] or [ft/min]
N_L - the number of rows of tubes
D - tube diameter in [m] or [ft]
S_T is the transverse tube pitch in [m] or [ft]
S_L is the longitudinal tube pitch in [m] or [ft]
Outputs
h - average heat transfer coefficient in [W/m^2-K] or [Btu/hr-ft^2-R]
deltap - total pressure drop in the pressure units set in the EES Unit System dialog
Nusselt - average Nusselt number [-], defined as
![]()
Re - Reynolds number [-], defined as
![]()
Notes
The procedure uses correlations and correction factors provided by Žukauskas (1972). These correlations apply for values of Reynolds numbers from ~30<Re<1e8 and Prandtl numbers from ~0.7<Pr<500. At Reynolds numbers 100<Re<1000, the heat transfer coefficient can be calculated assuming a single cylinder in crossflow. Under those conditions the Churchill and Bernstein correlation(1977) is used.
Experimental data verifying the correlations are limited in geometric layout to relative longitudinal pitches (S_L/D) between 1.25 and 2.5. The accuracy of values outside this range is uncertain.
The Reynolds and Prandtl number are based on fluid properties evaluated at the film temperature, which is the average of the free stream and the surface temperature.
Example
$unitSystem SI K Pa J
T_s=328 [K]
Fluid$='air'
P=101300 [Pa]
u_inf=0.9 [m/s]
D=0.5 [m]
T_in=370 [K]
T_out=350 [K]
N_L=13
S_T=1.1 [m]
S_L=1.0 [m]
Call External_Flow_Inline_Bank(Fluid$, T_in, T_out, T_s, P, u_inf, N_L, D,S_T,S_L: h, DELTAp, Nusselt, Re)
{Solution: h=10.79 [W/m^2-K], DELTAp=2.343 [Pa], Nusselt=179.7 [-], Re=38,058 [-]}