Contents
GearPump1_CL
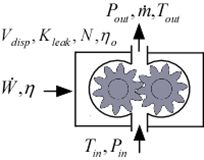
This procedure provides a simple model of a gear pump. The volumetric flow rate is determined from displacement rate less leakage flow. Power is determined from overall efficiency applied to displacement flow rate. The parameters V_disp, K_leak, and eta_o can be obtained from manufacturer's performance data.
Inputs:
F$: fluid string identifier
C: concentration (%) {applicable when F$ is a brine. Otherwise set C=0.}
T_in: inlet temperature (K, C, F, or R)
P_in: inlet pressure (bar, atm, Pa, kPa, MPa)
P_out: outlet pressure (bar, atm, Pa, kPa, MPa)
N: rotational speed (1/s)
V_disp: displacement of pump per cycle (in^3 or m^3)
K_leak: leakage constant (in^2 or m^2); if K_leak<0, then a typical value will be used
eta_o: overall efficiency of pump (-)
Outputs:
m_dot: mass flow rate (kg/s or lb_m/hr)
T_out: outlet temperature (K, C, F, or R)
W_dot: power (W, kW or Btu/hr)
eta_p: actual efficiency relative to power
eta_v: volumetric efficiency
Example 1:
$UnitSystem SI Mass kJ C kPa
T_in=25 [C]
P_in=100 [kPa]
P_out=500 [kPa]
F$='DowTherm_J'
N=1700 [1/min]*convert(1/min,1/s)
V_disp=0.06 [liter]*convert(liter,m^3)
K_leak=3 [mm^2]*Convert(mm^2,m^2)
eta_o=0.6 [-]
Call GearPump1_CL( F$, C, T_in, P_in, P_out, N, V_disp, K_leak, eta_o: m_dot, T_out, W_dot, eta_p, eta_v)
{Solution:
eta_p=0.5773
eta_v=0.9621
m_dot=1.418 [kg/s]
T_out=25.18 [C]
W_dot=1.133 [kW]}
Example 2:
$UnitSystem SI Mass kJ C kPa
T_in=25 [C]
P_in=100 [kPa]
P_out=500 [kPa]
F$='EG' {ethylene glycol - water solution}
C=20 [%]
N=1700 [1/min]*convert(1/min,1/s)
V_disp=0.06 [liter]*convert(liter,m^3)
K_leak=3 [mm^2]*Convert(mm^2,m^2)
eta_o=0.6 [-]
Call GearPump1_CL( F$, C, T_in, P_in, P_out, N, V_disp, K_leak, eta_o: m_dot, T_out, W_dot, eta_p, eta_v)
{Solution:
eta_p=0.5773
eta_v=0.9651
m_dot=1.677 [kg/s]
T_out=25.17 [C]
W_dot=1.133 [kW]}
See also: GearPump2_CL
Index
